这一篇测试一下移动图片+批量改图片内链脚本

Lab4-3同态加密实验

课程：大数据安全
组号：第9组
成员：王雨辰 2022211650 李孜炎 2022211651 肖壹夫 2022211655 徐同一 2022211657 张丽娜 2022211673

实验内容：
同态加密模块是数据安全教学实验中的一个重要模块，具体功能包括Paillier加法同态加密算法的实现、加法同态加密算法与典型的全同态加密算法之间性能比较分析、基于安全等级的密钥长度选取方法、经典问题（平均工资问题）的编程实现

1. Paillier加法同态加密算法的实现

原理

生成密钥对：Paillier加密算法需要生成公钥和私钥。首先需要选择两个大素数p和 q，计算 n=p×q，然后计算 λ=lcm(p−1,q−1)，生成公钥 (n,g)和私钥 λ。
加密：选择一个明文 m，然后计算加密密文 c:$$c=g^m\times r^n \ mod\ n^2$$其中，r 是一个随机数，且 r需要满足与 n互质。
加法同态性：Paillier加密支持加法同态性，即对于两个加密值 $c_1$和 $c_2$，可以通过以下操作计算加密后的结果：$$c_1 \times c_2 \mod n^2 = \text{Enc}(m_1 + m_2)$$这样，在加密后的数据上直接进行乘法操作，解密后即为明文相加的结果。
解密：使用私钥 λ 解密密文：$$m = \frac{L(c^\lambda \mod n^2)}{L(g^\lambda \mod n^2)} \mod n$$其中，$L(x) = \frac{x - 1}{n}$是一个特殊的函数。

验证：

from phe import paillier  
  
def paillier_homomorphic_addition():  
    # 生成 Paillier 密钥对  
    public_key, private_key = paillier.generate_paillier_keypair()  
  
    # 明文数  
    m1 = 100  
    m2 = 200  
  
    # 使用公钥加密明文数  
    encrypted1 = public_key.encrypt(m1)  
    encrypted2 = public_key.encrypt(m2)  
  
    # 同态加法（对加密的数进行加法运算）  
    encrypted_sum = encrypted1 + encrypted2  
  
    # 使用私钥解密同态加法结果  
    decrypted_sum = private_key.decrypt(encrypted_sum)  
  
    # 输出结果  
    print(f"Decrypted sum: {decrypted_sum}")  # 应该输出 300  
# 执行同态加法  
paillier_homomorphic_addition()

![[./Pasted image 20241115232100.png|Pasted image 20241115232100]]

2. 加法同态加密算法与典型的全同态加密算法之间性能比较分析

进行加法同态加密算法（如 Paillier）与 典型的全同态加密算法（如 BFV、CKKS 等）的性能比较分析，涉及多个方面的考量，包括加密/解密速度、同态运算的效率、密文大小、适用场景等。全同态加密（FHE，Fully Homomorphic Encryption）是支持加法和乘法等多种同态操作的加密方案，而加法同态加密（如 Paillier）只支持加法操作。

2.1 加解密速度比较分析

加法同态加密（如 Paillier）：
- Paillier 加密算法只支持加法同态运算，因此加密和解密速度相对较快，特别是在处理大批量数据时，效率较高。
- 加密操作通常是基于指数运算，解密操作相对较简单，通常涉及一个模逆运算。
- 由于只支持加法，同态加法操作通常比较快速，适合处理一些对加法比较密集的任务（如统计计算、隐私保护的加法操作等）。
全同态加密（如 BFV、CKKS）：
- 全同态加密支持加法、乘法、以及更多复杂的运算，因此其加密和解密的计算复杂度较高。
- 在支持多种同态运算时，解密过程往往需要多次密文解压、归约和解密，计算负担较大。
- 由于全同态加密支持多种运算，它的加密和解密时间会显著大于加法同态加密。

代码（使用phe库版）

compare.py

import time  
import phe  
import tenseal as ts  
  
# ======================= 优化后的 Paillier 加法同态加解密 =======================def paillier_encryption_batch(values):  
    # 创建 Paillier 密钥对  
    public_key, private_key = phe.generate_paillier_keypair()  
  
    # 批量加密数据  
    encrypted_values = [public_key.encrypt(value) for value in values]  
  
    # 同态加法  
    encrypted_sum = encrypted_values[0]  
    for enc_value in encrypted_values[1:]:  
        encrypted_sum += enc_value  # 批量加法  
  
    return encrypted_sum, public_key, private_key  
  
def paillier_decryption(encrypted_value, private_key):  
    # 解密数据  
    decrypted_value = private_key.decrypt(encrypted_value)  
    return decrypted_value  
  
# ======================= 全同态加解密（TenSEAL - CKKS） =======================def full_homomorphic_encryption(value1, value2, context):  
    # 创建 CKKS 向量并加密  
    encrypted_value1 = ts.ckks_vector(context, [value1])  
    encrypted_value2 = ts.ckks_vector(context, [value2])  
  
    # 同态加法  
    encrypted_sum = encrypted_value1 + encrypted_value2  
    return encrypted_sum  
  
def full_homomorphic_decryption(encrypted_value, secret_key):  
    # 解密数据  
    decrypted_value = encrypted_value.decrypt(secret_key)  
    return decrypted_value[0]  
  
# ======================= 实验代码：比较加法同态和全同态加解密速度 =======================# Paillier 加法同态加解密（优化版）  
def paillier_test():  
    # 测试数据  
    values = [15, 20]  
  
    # 计时  
    start_time = time.time()  
    encrypted_sum, public_key, private_key = paillier_encryption_batch(values)  
    decrypted_sum = paillier_decryption(encrypted_sum, private_key)  
    end_time = time.time()  
  
    # 输出 Paillier 加解密结果  
    print(f"Paillier 加解密时间: {end_time - start_time} 秒")  
    print(f"Paillier 解密结果: {decrypted_sum}")  
    return end_time - start_time  # 返回加解密时间  
  
# 全同态加解密（TenSEAL - CKKS）  
def full_homomorphic_test():  
    # 创建 TenSEAL 上下文，初始化加密参数  
    context = ts.context(ts.SCHEME_TYPE.CKKS, poly_modulus_degree=8192, coeff_mod_bit_sizes=[60, 40, 60])  
    context.global_scale = 2**40  # 设置 global scale    context.generate_galois_keys()  # 生成 Galois 密钥  
    secret_key = context.secret_key()  
  
    # 测试数据  
    value1, value2 = 15, 20  
  
    # 计时  
    start_time = time.time()  
    encrypted_sum = full_homomorphic_encryption(value1, value2, context)  
    decrypted_sum = full_homomorphic_decryption(encrypted_sum, secret_key)  
    end_time = time.time()  
  
    # 输出 TenSEAL 加解密结果  
    print(f"全同态加解密时间: {end_time - start_time} 秒")  
    print(f"全同态解密结果: {decrypted_sum}")  
    return end_time - start_time  # 返回加解密时间  
  
# ======================= 主程序：比较 Paillier 和 TenSEAL 的性能 =======================if __name__ == "__main__":  
    # 比较加法同态加解密时间（Paillier）  
    paillier_time = paillier_test()  
  
    # 比较全同态加解密时间（TenSEAL）  
    full_homomorphic_time = full_homomorphic_test()  
  
    # 输出对比结果  
    print(f"\n实验结果：")  
    print(f"Paillier 加法同态加解密时间: {paillier_time} 秒")  
    print(f"全同态加解密时间 (TenSEAL): {full_homomorphic_time} 秒")

代码（gmpy2）

compare2.py
这个版本使用gmpy2库自定义实现paillier，相比于上个版本使用phe库标准的paillier实现，加解密速度快了许多
原因：

- gmpy2 的使用：手动实现中使用 gmpy2 来处理大整数运算，这个库在性能上远远优于 Python 的默认整数运算，因为它底层使用了 GMP 库（一个高性能的多精度算术库），专门用于大数运算。而 phe 库通常使用 Python 原生的大整数对象，运算效率较低。

随机数生成优化：使用 random.SystemRandom() 提供系统级的随机数生成，结合 gmpy2.next_prime() 来迅速找到合适的大素数，这减少了冗余计算，提升了密钥生成效率。

@staticmethod
def _get_prime_over(N):
    rand_func = random.SystemRandom()
    r = gmpy2.mpz(rand_func.getrandbits(N))
    r = gmpy2.bit_set(r, N - 1)
    return int(gmpy2.next_prime(r))

gmpy2.powmod() 是直接在整数层面进行快速幂运算和取模操作，这在加密过程中的计算 g^m % n^2 和 r^n % n^2 非常高效。相比之下，phe 库的实现可能会包含额外的类型检查和更复杂的逻辑，这会增加计算时间。

def encrypt(self, m):
    r = random.randint(1, self.public_key.n - 1)
    cipher_text = gmpy2.mod(
        gmpy2.powmod(self.public_key.g, m, self.n_square) * gmpy2.powmod(r, self.public_key.n, self.n_square),
        self.n_square)
    cipher_text = CryptoNumber(cipher_text, self.n_square)
    return cipher_text

import time  
import tenseal as ts  
import random  
from collections import namedtuple  
import gmpy2  
  
# ======================= Paillier 密钥生成 =======================class PaillierKeyGenerator:  
    @staticmethod  
    def _get_prime_over(N):  
        rand_func = random.SystemRandom()  
        r = gmpy2.mpz(rand_func.getrandbits(N))  
        r = gmpy2.bit_set(r, N - 1)  
        return int(gmpy2.next_prime(r))  
  
    @staticmethod  
    def _generate_p_q(key_size):  
        p = q = None  
        n_len = 0  
        while n_len != key_size:  
            p = PaillierKeyGenerator._get_prime_over(key_size // 2)  
            q = p  
            while q == p:  
                q = PaillierKeyGenerator._get_prime_over(key_size // 2)  
            n = p * q  
            n_len = n.bit_length()  
        return p, q  
  
    @staticmethod  
    def generate_keypair(key_size):  
        p, q = PaillierKeyGenerator._generate_p_q(key_size)  
        n = p * q  
        lam = gmpy2.lcm(p - 1, q - 1)  
  
        n_square = pow(n, 2)  
        g = n + random.randint(n, n_square - 1)  
        fn_L = lambda x, n: (x - 1) // n  
        mu = gmpy2.invert(fn_L(gmpy2.powmod(g, lam, n_square), n), n)  
        while gmpy2.gcd(g, n_square) != 1:  
            g = n + random.randint(n, n_square - 1)  
        PublicKey = namedtuple("PublicKey", "n g")  
        PrivateKey = namedtuple("PrivateKey", "public_key lam mu")  
        public_key = PublicKey(n=n, g=g)  
        private_key = PrivateKey(public_key=public_key, lam=lam, mu=mu)  
        return public_key, private_key  
  
# ======================= Paillier 加解密 =======================class Paillier:  
    CIPHER_MODE_ENCRYPT = 0  
    CIPHER_MODE_DECRYPT = 1  
    cipher = None  
  
    def __init__(self, cipher_mode, cipher_key):  
        if cipher_mode == Paillier.CIPHER_MODE_ENCRYPT:  
            self.public_key = cipher_key  
            self.private_key = None  
        elif cipher_mode == Paillier.CIPHER_MODE_DECRYPT:  
            self.public_key = cipher_key.public_key  
            self.private_key = cipher_key  
        else:  
            raise ValueError('cipher_mode value must be either CIPHER_MODE_ENCRYPT or CIPHER_MODE_DECRYPT')  
        self.cipher_mode = cipher_mode  
        self.n_square = pow(self.public_key.n, 2)  
  
    def fn_L(self, x):  
        return (x - 1) // self.public_key.n  
  
    def encrypt(self, m):  
        r = random.randint(1, self.public_key.n - 1)  
        cipher_text = gmpy2.mod(  
            gmpy2.powmod(self.public_key.g, m, self.n_square) * gmpy2.powmod(r, self.public_key.n, self.n_square),  
            self.n_square)  
        cipher_text = CryptoNumber(cipher_text, self.n_square)  
        return cipher_text  
  
    def decrypt(self, crypto_number):  
        numerator = self.fn_L(gmpy2.powmod(crypto_number.cipher_text, self.private_key.lam, self.n_square))  
        numerator = gmpy2.mod(numerator * self.private_key.mu, self.public_key.n)  
        return numerator  
  
    def __str__(self):  
        return Paillier.cipher  
  
# ======================= 同态运算 =======================class CryptoNumber:  
    def __init__(self, cipher_text, n_square):  
        self.cipher_text = cipher_text  
        self.n_square = n_square  
  
    def __add__(self, other):  
        if isinstance(other, CryptoNumber):  
            sum_ciphertext = gmpy2.mod(self.cipher_text * other.cipher_text, self.n_square)  
            return CryptoNumber(sum_ciphertext, self.n_square)  
        else:  
            raise TypeError('Unsupported operand type(s) for +: "CryptoNumber" and "{}"'.format(type(other)))  
  
    def __mul__(self, other):  
        if isinstance(other, CryptoNumber):  
            raise NotImplementedError('Multiplication between two "CryptoNumber" instances is not supported')  
        else:  
            mul_cipher_text = gmpy2.mod(pow(self.cipher_text, other), self.n_square)  
            return CryptoNumber(mul_cipher_text, self.n_square)  
  
# ======================= 优化后的 Paillier 加法同态加解密 =======================def paillier_encryption_batch(values, public_key):  
    paillier = Paillier(Paillier.CIPHER_MODE_ENCRYPT, public_key)  
    # 批量加密数据  
    encrypted_values = [paillier.encrypt(value) for value in values]  
    return encrypted_values  
  
def paillier_homomorphic_addition(encrypted_values):  
    encrypted_sum = encrypted_values[0]  
    for enc_value in encrypted_values[1:]:  
        encrypted_sum += enc_value  # 同态加法  
    return encrypted_sum  
  
def paillier_decryption(encrypted_value, private_key):  
    paillier = Paillier(Paillier.CIPHER_MODE_DECRYPT, private_key)  
    # 解密数据  
    decrypted_value = paillier.decrypt(encrypted_value)  
    return decrypted_value  
  
def paillier_test(public_key, private_key):  
    # 测试数据  
    values = [15, 20]  
  
    # 计时开始  
    start_time = time.time()  
  
    # 加密数据  
    encrypted_values = paillier_encryption_batch(values, public_key)  
  
    # 同态加法  
    encrypted_sum = paillier_homomorphic_addition(encrypted_values)  
  
    # 解密结果  
    decrypted_sum = paillier_decryption(encrypted_sum, private_key)  
  
    # 计时结束  
    end_time = time.time()  
  
    # 输出结果  
    print(f"Paillier 加解密时间: {end_time - start_time} 秒")  
    print(f"Paillier 解密结果: {decrypted_sum}")  
    return end_time - start_time  
  
# ======================= 全同态加解密（TenSEAL - CKKS） =======================def full_homomorphic_encryption(value1, value2, context):  
    # 创建 CKKS 向量并加密  
    encrypted_value1 = ts.ckks_vector(context, [value1])  
    encrypted_value2 = ts.ckks_vector(context, [value2])  
  
    # 同态加法  
    encrypted_sum = encrypted_value1 + encrypted_value2  
    return encrypted_sum  
  
def full_homomorphic_decryption(encrypted_value, secret_key):  
    # 解密数据  
    decrypted_value = encrypted_value.decrypt(secret_key)  
    return decrypted_value[0]  
  
def full_homomorphic_test(context, secret_key):  
    # 测试数据  
    value1, value2 = 15, 20  
  
    # 计时开始  
    start_time = time.time()  
  
    # 加密和同态加法  
    encrypted_sum = full_homomorphic_encryption(value1, value2, context)  
  
    # 解密结果  
    decrypted_sum = full_homomorphic_decryption(encrypted_sum, secret_key)  
  
    # 计时结束  
    end_time = time.time()  
  
    # 输出结果  
    print(f"全同态加解密时间: {end_time - start_time} 秒")  
    print(f"全同态解密结果: {decrypted_sum}")  
    return end_time - start_time  
  
# ======================= 主程序：比较 Paillier 和 TenSEAL 的性能 =======================if __name__ == "__main__":  
    # ===== Paillier 密钥生成（不计入时间）=====  
    public_key, private_key = PaillierKeyGenerator.generate_keypair(1024)  
  
    # 比较加法同态加解密时间（Paillier）  
    paillier_time = paillier_test(public_key, private_key)  
  
    # ===== TenSEAL 上下文和密钥生成（不计入时间）=====  
    context = ts.context(ts.SCHEME_TYPE.CKKS, poly_modulus_degree=8192, coeff_mod_bit_sizes=[60, 40, 60])  
    context.global_scale = 2**40  # 设置 global scale    context.generate_galois_keys()  # 生成 Galois 密钥  
    secret_key = context.secret_key()  
  
    # 比较全同态加解密时间（TenSEAL）  
    full_homomorphic_time = full_homomorphic_test(context, secret_key)  
  
    # 输出对比结果  
    print(f"\n实验结果：")  
    print(f"Paillier 加法同态加解密时间: {paillier_time} 秒")  
    print(f"全同态加解密时间 (TenSEAL): {full_homomorphic_time} 秒")

![[./Pasted image 20241116144236.png|Pasted image 20241116144236]]

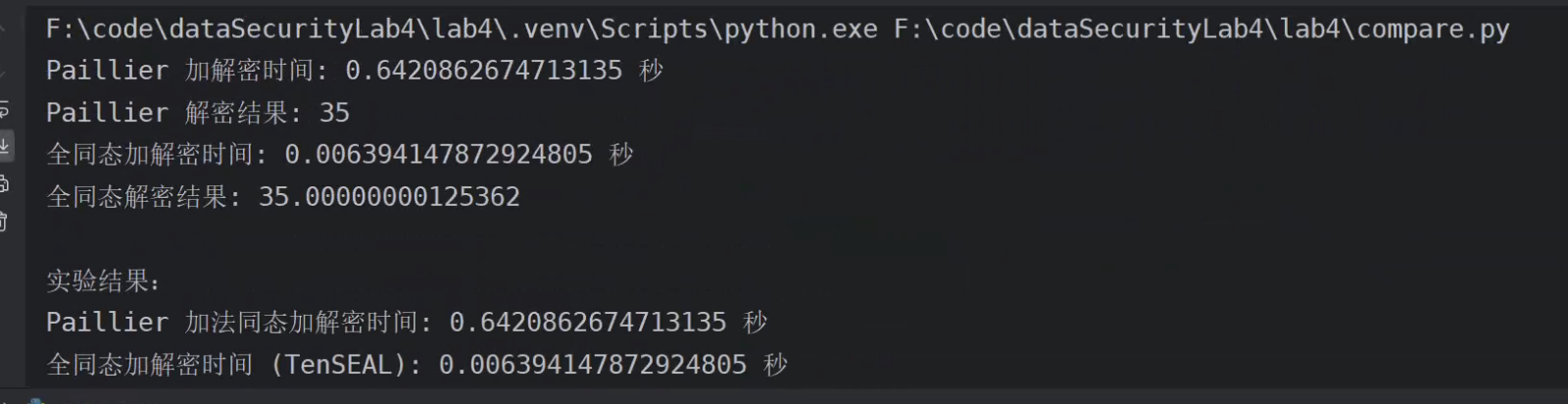
分析
- 加解密时间
  - 在不计入密钥生成时间的情况下，Paillier 加解密的时间显著小于全同态加密（TenSEAL）的加解密时间。
- 解密结果
  - 加法同态解密结果是精确的，而全同态的解密结果与预期结果存在微小误差
  - 原因：TenSEAL 使用的 CKKS 同态加密方案是一种近似计算的算法，主要用于处理浮点数和机器学习中的计算。由于CKKS的设计特点，同态运算过程中会引入少量的误差，尤其是在进行乘法和复杂运算时。这就是为什么解密结果不是精确的 35，而是一个非常接近 35 的浮点数。
  - 如果需要在 TenSEAL 中得到更精确的结果，可以尝试调整加密参数，例如增大 global_scale，但这可能会增加计算时间和内存开销。
- 根据应用需求选择合适的加密方案。Paillier 适用于需要精确计算的场景，CKKS 更适合处理浮点数和需要大量同态运算的机器学习任务。

增加同态运算的复杂度
在 TenSEAL 中，增加更多的同态运算（如同态乘法、平方）可以延长加解密时间。

def full_homomorphic_encryption(value1, value2, context):
    # 创建 CKKS 向量并加密
    encrypted_value1 = ts.ckks_vector(context, [value1])
    encrypted_value2 = ts.ckks_vector(context, [value2])
    # 同态加法
    encrypted_sum = encrypted_value1 + encrypted_value2
    # 增加同态乘法
    encrypted_product = encrypted_sum * encrypted_value1
    # 增加同态平方
    encrypted_result = encrypted_product.square()
    return encrypted_result

![[./Pasted image 20241117154800.png|Pasted image 20241117154800]]

2.2 密文大小的比较

Paillier（加法同态加密）

Paillier 加密方案是一种加法同态加密方案，支持加法操作的同态运算。其密文的大小主要由模数 nnn 和 n2n^2n2 的位长度决定。

密钥生成：Paillier 的密钥生成依赖于两个大素数 p 和 q，计算出模数 $n = p \times q和 n^2$，其密文的大小大约为$2 \times \text{bit length of } n$，即大约是 $2 \times \text{key size in bits}$。
密文大小：通常，Paillier 密文的大小为 2048 位或 4096 位，具体取决于密钥大小。对于 1024 位的密钥，密文的大小大约为 2048 位。
计算公式：$$
\text{密文大小} \approx 2 \times (\text{key size in bits})$$
如果使用 2048 位的密钥，密文的大小大约是 4096 位。

全同态加密（如 BFV 和 CKKS）

全同态加密（FHE）允许对密文进行任意数量的同态运算（包括加法、乘法等）。典型的全同态加密方案如 BFV 和 CKKS，它们的密文大小通常更大，因为它们支持更复杂的操作，并且涉及更多的加密参数。
###### BFV 加密方案
- 多项式表示：BFV 使用多项式环进行加密，密文包含多项式的系数。每个系数的大小通常是由系数模数决定的。
- 密文大小：BFV 密文的大小由以下几个参数决定：
1. 多项式度数：多项式度数 N 决定了密文中的多项式的长度。
2. 系数模数：系数模数的位数决定了每个系数所需的位数。
对于 BFV，假设多项式度数为 N，每个系数的模数大小为B，则密文的大小大致为：
$$\text{密文大小} \approx N \times \text{位数}(\text{系数模数})$$

比如，选择 N = 8192，每个系数模数为 60 位，则密文大小大约是 $8192 \times 60$位，即约 491,520 位。
###### CKKS 加密方案
- 多项式表示：CKKS 是一种专门针对近似同态加密设计的加密方案，支持浮点数的加密。与 BFV 类似，CKKS 使用多项式表示，但它在加密时采用了近似技术。

- 密文大小：与 BFV 类似，CKKS 的密文大小也由多项式度数和系数模数大小决定。

对于 CKKS，假设多项式度数为 NNN，系数模数大小为 BBB，则密文的大小大致为：$$\text{密文大小} \approx N \times \text{位数}(\text{系数模数})$$
如果选择 N = 8192，每个系数模数为 60 位，则密文大小大约是 8192 \times 60 位，即约 491,520 位。

加密方案	密文大小（密钥大小 1024 位）	特点
Paillier	2048 位（密钥大小 1024 位）	仅支持加法同态，适合简单的加法运算
BFV	491,520 位（8192 多项式度数，60 位系数模数）	支持加法和乘法同态，计算复杂度较高
CKKS	491,520 位（8192 多项式度数，60 位系数模数）	支持加法和乘法同态，适用于近似同态计算

结论：

Paillier：适用于加法同态，密文相对较小，通常为 2048 位或 4096 位，适合处理加法操作，但不支持乘法。
BFV/CKKS：作为全同态加密方案，密文大小显著更大，通常在几百千位，适合执行更复杂的加法和乘法同态操作。

密文大小的影响：

Paillier：因为仅支持加法同态，因此密文较小，适用于隐私保护需要较少计算量的场景。
全同态加密（如 BFV、CKKS）：虽然密文更大，但它们可以执行更加复杂的同态操作（加法、乘法等），适用于需要进行复杂计算（如加密计算、隐私保护机器学习）的场景。

2.3 适用场景

1. 加法同态加密（Additive Homomorphic Encryption）

适用场景：

加密数据的求和与计数：
- 金融分析：在多个加密的交易数据（如账户余额、支付记录）上进行加法运算，得到加密的总额或总计数。例如，多个公司或个人可以将自己的财务数据加密后提交，进行合并、汇总或统计，而不会暴露具体的财务数据。
- 电子投票：电子投票系统可以使用加法同态加密技术来实现加密的投票统计，确保每个投票人的隐私，同时能够对投票结果进行合并和统计。
- 统计分析：进行数据汇总、加权求和等操作时，适合使用加法同态加密。例如，政府、银行等机构进行加密数据的统计分析，能够保持数据的隐私。
- 医疗健康数据分析：多个医院或医疗机构可以使用加法同态加密分析不同患者的健康数据，进行加密汇总分析，而不会泄露患者的个人隐私。
简单的加法运算：
- 加法同态加密适用于需要对加密数据进行简单的加法操作的场景。例如，在多个加密数据的加总或加权求和中非常高效。
  优势：
计算效率较高：相对于全同态加密，加法同态加密的计算复杂度较低，尤其在进行简单的加法运算时，性能较好。
广泛应用于统计和汇总场景：适用于各种涉及合并、加总、计数等简单加法运算的任务。
局限性：
功能有限：仅支持加法操作，无法执行乘法、比较等其他复杂运算。因此，若任务涉及复杂的运算，无法仅通过加法同态加密完成。

2. 全同态加密（Fully Homomorphic Encryption, FHE）

适用场景：

复杂的加法和乘法运算：
- 安全计算与联合学习：在多个参与方之间进行联合机器学习、数据分析等任务时，每个参与方的数据需要保持私密。全同态加密可以支持对加密数据进行复杂的运算（加法、乘法、矩阵运算等），从而实现数据共享与隐私保护的平衡。
- 加密数据库查询：全同态加密可用于对加密数据进行复杂查询，例如加密的数据库中进行加法、乘法、聚合等操作，返回加密的查询结果。这对于加密数据库的隐私保护和合规性要求至关重要。
- 安全多方计算：例如，在去中心化的金融（DeFi）系统中，多个独立的参与方可以用全同态加密协议执行计算（如资产计算、风险评估等），保证数据隐私的同时完成复杂的计算任务。
- 生物信息学与基因数据分析：全同态加密可以保护基因数据的隐私，在加密的基因组数据上进行计算，如基因比对、遗传算法等，避免敏感数据泄漏。
隐私保护的机器学习与人工智能：
- 全同态加密使得机器学习和AI算法能够在加密数据上直接执行，不必解密数据。例如，使用加密数据训练模型或在加密数据上做推理，保证数据隐私同时进行智能分析。
加密数据的复杂处理：
- 智能合约：在区块链智能合约中，全同态加密可以使得合约能够在加密状态下处理更复杂的逻辑，例如加密的数据计算、验证等任务。
  优势：
支持复杂运算：全同态加密不仅支持加法，还支持乘法及其他更复杂的运算，非常适合涉及复杂数据处理的场景。
强隐私保护：可以在完全不暴露数据的情况下执行复杂计算，保障数据的隐私性。
局限性：
计算开销较大：全同态加密的计算和加密密文的大小相对较大，因此效率较低，不适合处理非常大规模的数据或实时性要求较高的任务。
实现复杂：全同态加密的实现较为复杂，通常需要专门的硬件或优化的计算环境来提升性能。

2.4 加法同态加密 vs 全同态加密：对比总结

特性	加法同态加密	全同态加密
支持运算类型	仅支持加法操作	支持加法、乘法等任意运算
计算复杂度	较低，运算效率较高	较高，运算效率低
适用场景	数据汇总、统计、加权求和、计数等简单加法运算	安全计算、机器学习、复杂查询、加密数据库等复杂运算
隐私保护	保证数据隐私，但只限于加法计算	更强的隐私保护，支持复杂的加密数据处理
密文大小	相对较小	相对较大
计算能力	高效且适合简单任务	适合复杂任务，但开销较大
技术复杂度	实现较简单	实现复杂，通常需要特殊优化

3.基于安全等级的密钥长度选取方法

3.1 Paillier加密的密钥长度选取

Paillier 加密是一种加法同态加密方案，其安全性通常基于大数分解的困难性（特别是整数分解问题）。

Paillier加密的安全性分析

Paillier 加密的安全性主要依赖于生成的两个大素数的保密性。
密钥长度的选择通常基于目标的安全等级（例如 128 位、192 位或 256 位的安全性）。

密钥长度的选取方法

Paillier加密的密钥长度通常是通过两个素数（p 和 q）的位数来确定的。密钥的大小大致等于两个素数的乘积 n = p * q 的位数
128位安全性：
对于 128位安全性，选择 1024位的密钥长度是常见的做法。这意味着选择两个 512位的大素数 p 和 q 来生成密钥。这个长度适合一般的商业应用，如在线支付、数据加密等。
192位安全性：
如果你需要更高的安全性，可以选择 1536位的密钥长度，意味着每个素数的位数大约是 768位。这个长度适用于对安全性要求更高的场合，如金融交易、机密数据处理等。
256位安全性：
对于 256位安全性，可以选择 2048位的密钥长度，即每个素数的位数是 1024位。这个长度适用于高安全需求的环境，如国家安全、军事数据保护等。

3.2 全同态加密（FHE）基于BFV、CKKS的密钥长度选取

全同态加密（FHE）方案，如 BFV（Brakerski/Fan-Vikuntanathan）和 CKKS（Cheon-Kim-Kim-Song），它们的安全性依赖于“学习与误差”（LWE）假设或其他数学难题。FHE方案的安全性通常通过密钥和参数的大小来保证。

密钥长度选择的影响因素

多项式度数（Poly Modulus Degree）：
- 多项式度数通常以2的幂次方表示。常见的度数有 1024, 2048, 4096, 8192 等
- 这决定了密文的大小，度数越大，密文越大，计算能力要求越高。通常，选择更高的度数以提高安全性，但也会带来更高的计算成本。
- 多项式度数也与同态操作的效率相关。多项式度数越大，支持的同态操作（如加法、乘法等）就越多，但计算复杂度和存储需求也会增加。
- 决定了多项式的长度，即参与计算的系数的数量。
系数模数（Coeff Mod Bit Sizes）：
- 常见的位数有 60 位、40 位、20 位等
- 这是指每个加密数的大小，位数越高，表示每个数可以存储更大的值，因此也提高了安全性。
- 系数模数影响加密过程中数值的“噪声”水平。噪声过大可能会导致解密错误，因此系数模数的选择必须平衡安全性和噪声管理。
- 决定了每个多项式系数的大小和范围，通常需要大于多项式的大小。

BFV加密的密钥长度选取

BFV 加密方案广泛应用于加密计算和同态运算。BFV 的安全性依赖于 大整数的分解问题 和 噪声的积累。

加密安全性：选择 BFV 时，密钥大小和多项式的度数决定了安全性等级。
密钥长度与安全等级：
- 128 位安全性：推荐使用 2048 位或 3072 位的公钥和密钥长度。
- 192 位安全性：通常选择 4096 位或更长的密钥。
- 256 位安全性：使用更长的密钥（如 8192 位及以上）。

CKKS加密的密钥长度选取

CKKS 是针对近似同态加密（Approximate Homomorphic Encryption, AHE）的一种方案，特别适用于连续数据如浮点数加密。它基于 LWE（学习带误差）假设。

加密安全性：CKKS 加密的安全性同样依赖于多项式的度数和系数模数。CKKS 的密钥选择通常与 poly_modulus_degree（多项式度数）和 coeff_mod_bit_sizes（系数模数）相关。
常见的参数选择：
- 128 位安全性：常见的选择是 poly_modulus_degree = 8192 和 **coeff_mod_bit_sizes = [60, 40, 60]**。
- 192 位安全性：通常选择更大的多项式度数，如 poly_modulus_degree = 16384 和 **coeff_mod_bit_sizes = [60, 40, 60]**。
- 256 位安全性：可能选择 poly_modulus_degree = 32768 和 **coeff_mod_bit_sizes = [60, 40, 60]**。

下面是一个基于安全等级选择密钥长度的推荐方法：

安全等级	多项式度数（poly_modulus_degree）	系数模数（coeff_mod_bit_sizes）
128位安全性	8192	[60, 40, 60]
192位安全性	16384	[60, 50, 60]
256位安全性	16384	[80, 60, 80]

4. 经典问题的编程实现

import tenseal as ts

# 1. 初始化 TenSEAL 上下文
context = ts.context(ts.SCHEME_TYPE.CKKS, poly_modulus_degree=8192, coeff_mod_bit_sizes=[60, 40, 60])
context.generate_galois_keys()

# 2. 设置 global_scale
context.global_scale = 2**60  # 设置较大的 global scale，通常为 2 的较大次幂

# 3. 模拟一些工资数据
# 假设有5个员工的工资
salaries = [5000, 5500, 6000, 6500, 7000]

# 4. 对工资数据进行加密
# 使用 TenSEAL 的 ckks_vector 进行加密
encrypted_salaries = [ts.ckks_vector(context, [salary]) for salary in salaries]

# 5. 计算加密工资的总和（同态加法）
encrypted_sum = encrypted_salaries[0]
for encrypted_salary in encrypted_salaries[1:]:
    encrypted_sum = encrypted_sum + encrypted_salary

# 6. 计算总和的平均工资（解密得到结果）
# 计算总和之后除以工资数量
decrypted_sum = encrypted_sum.decrypt()
decrypted_average = decrypted_sum[0] / len(salaries)

# 7. 输出结果
print(f"Encrypted total sum of salaries: {decrypted_sum[0]}")
print(f"Encrypted average salary: {decrypted_average}")

![[./Pasted image 20241117212240.png|Pasted image 20241117212240]]